In questa lezione vediamo il cambio di variabile per gli integrali doppi (coordinate polari e coordinate ellittiche) e la definizione di diffeomorfismo.
Teorema del cambio di variabile (integrali doppi)
Nel teorema si parlerà di diffeomorfismo. Vedremo dopo la definizione di diffeomorfismo perché adesso ci concentriamo sul teorema.
Dato un insieme regolare Ω⊆ R2 e una funzione f∈ C(Ω), definiamo la seguente funzione:

Se la funzione Φ è un diffeomorfismo allora:

La matrice J è la jacobiana. Ora vediamo la spiegazione.
In pratica il teorema ci dà un metodo per fare un cambio di variabile. Ci dice che dobbiamo prendere una funzione Φ che è definita in modo tale da avere x=g(u,v) e y=h(u,v) e se è un diffeomorfismo (tra poco vediamo cosa vuol dire) allora possiamo fare il cambio di variabile: al posto di x e di y che erano nella funzione f(x,y) scriviamo g(u,v) e h(u,v); inoltre nell’integrale dobbiamo moltiplicare per il modulo del determinante della jacobiana di Φ.
Sembra tutto strano e difficile ma tra poco vediamo un esempio per chiarire i dubbi.
diffeomorfismo: definizione
Una funzione Φ: Ω’ → Ω è un diffeomorfismo se valgono le seguenti tre proprietà:
- Φ è biettiva.
- Φ è di classe C1 su un insieme aperto che contiene Ω’.
- det(JΦ) ≠ 0 e limitato su Ω’.
State tranquilli, di solito si usano cambi di variabile standard (coordinate polari o ellittiche) e quindi queste proprietà non si controllano.
Se vogliamo essere rigorosi, ogni volta che facciamo un cambio di variabile dobbiamo controllare queste proprietà, ma si fa raramente: tranne in casi particolari (e masochistici) le proprietà sono verificate.
esempio 1
Ci chiediamo quanto vale l’area del seguente insieme:

Nella seconda riga abbiamo solo moltiplicato per x nel primo intervallo e diviso per x nel secondo. Otteniamo così due cose strane: la x e la y sono legate insieme, non abbiamo due intervalli separati (uno per la x e uno per la y). Forse qui è utile un cambio di variabile.
Che cambio di variabile facciamo? Potremmo porre xy = v e y/x = u. Attenzione però: per fare la jacobiana dobbiamo trovare la x e la y, infatti nel teorema ci dicono che x=g(u,v) e y=h(u,v).
Scriviamo:

C’è un solo passaggio strano: quando troviamo la x nella prima equazione facciamo una radice quindi davanti alla radice dobbiamo scrivere “±”. Tuttavia il segno “-” non è accettabile perché l’insieme Ω se lo disegnate ha la x>0. Il disegno è questo:

Ora abbiamo trovato la nostra x=g(u,v) e la nostra y=h(u,v).
Andiamo a calcolare il determinante della Jacobiana:
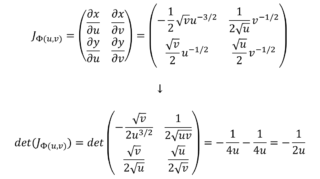
Le derivate non sono divertenti ma basta sfruttare le regole fondamentali, ricordando che la derivata rispetto ad u si fa considerando la v costante mentre la derivata rispetto a v si fa considerando la u costante. Poi si calcola il determinante.
A questo punto abbiamo quasi tutto. Ma qual è il nuovo insieme Ω’? Eccolo qua:
![]()
L’insieme è stato ottenuto a partire da Ω sostituendo xy=v e y/x=u.
Notiamo che u>0 sempre quindi il determinante che abbiamo calcolato sarà di sicuro <0. Quando facciamo il suo modulo, quindi, elimineremo il segno “-“.
Ricordando che per calcolare l’area basta integrare un “1” in dxdy scriviamo:
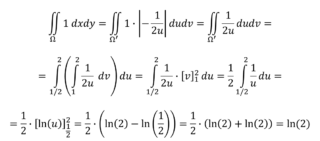
Abbiamo solo svolto l’integrale doppio. Nell’ultimo passaggio abbiamo sfruttato le proprietà dei logaritmi: ln(1/2)=ln(2-1)=-ln(2).
Se avessimo avuto una funzione più complicata di un banale “1” avremmo dovuto sostituire all’interno di quella funzione le formule per x e per y calcolate dopo aver posto xy=v e y/x=u (cioè quelle con le radici).
Come vedete, una corretta sostituzione migliora molto l’integrale da fare.
Adesso vedremo due classiche sostituzioni (o cambi di variabile): le coordinate polari e quelle ellittiche.
Coordinate polari
Scriveremo subito le formule per le coordinate polari e poi verificheremo che la funzione Φ che abbiamo scelto è un diffeomorfismo. Infine scriveremo l’integrale doppio che si ottiene dopo il cambio di variabile.
La formula per le coordinate polari è la seguente:
![]()
In pratica, ad un punto di coordinate (x,y) noi associamo un raggio ρ e un angolo θ come nella seguente figura:

Abbiamo quindi definito una funzione di questo tipo:
![]()
Per individuare un qualsiasi punto nel piano dobbiamo fare in modo che θ possa fare un giro completo (così riusciamo a beccare un punto ovunque sia), quindi metteremo θ∈ [0,2π). Inoltre si pone ρ∈ (0,+∞).
Ora cerchiamo di capire se quello che abbiamo definito è un diffeomorfismo: dobbiamo vedere se sono verificate le tre proprietà che abbiamo detto all’inizio della lezione.
- Φ è biiettiva?
Dobbiamo capire se la funzione che abbiamo definito associa ad ogni punto (x,y) una sola coppia di valori (ρ,θ). In pratica, ci domandiamo se ad un punto del piano attribuiamo solo un valore di ρ e uno di θ. E’ facile intuire che di sicuro per ogni punto che prendiamo riusciremo a trovare una sola coppia (ρ,θ).
La funzione Φ è quindi biiettiva. - Φ è di classe C1 su un aperto contenente Ω’?
La funzione è di classe C1 perché è formata da seni e coseni, che sono di classe C1. Tuttavia Ω’ non è aperto perché quando abbiamo definito θ abbiamo messo θ∈ [0,2π). Per farlo diventare aperto poniamo θ∈ (0,2π). Questo passaggio non crea problemi nell’integrale che dobbiamo fare perché abbiamo tolto un insieme di misura nulla (θ=0) e sappiamo (dalla Lezione 19) che gli insiemi di misura nulla non influenzano l’integrale. - Il determinante della jacobiana è diverso da zero?
Dobbiamo calcolarlo. Ricordiamo che per la jacobiana dobbiamo avere le funzioni scritte come x=… e y=… quindi noi, grazie al sistema che abbiamo scritto poco fa, ce le abbiamo già nella forma corretta e possiamo derivarle.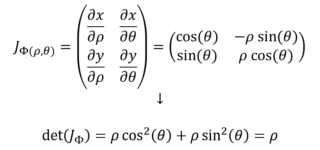
Siccome abbiamo definito ρ ponendolo > 0, esso sarà di sicuro diverso da zero e quindi il determinante è sempre diverso da zero.
Abbiamo quindi che la funzione Φ è un diffeomorfismo.
Possiamo quindi fare il cambio di variabile e l’integrale risultante è questo:

Come vedete, siccome ρ>0, il modulo di ρ è semplicemente ρ.
Le coordinate polari sono standard e si utilizzano quando l’insieme Ω ha una forma simile ad un cerchio (es. settore circolare, corona circolare, cerchio).
Coordinate ellittiche
Le coordinate ellittiche si usano raramente ma è meglio farle perché non si sa mai.
Si utilizzano quando l’insieme Ω su cui bisogna integrare la funzione f(x,y) è un’ellisse, la cui equazione è:
![]()
Le coordinate ellittiche sono le seguenti:
![]()
Per definizione θ∈ (0,2π), ρ∈ (0,+∞).
Se sostituiamo le due formule all’interno dell’equazione dell’ellisse otteniamo ρ2 ≤ 1, che risolta dà come risultato -1 ≤ ρ ≤ 1. Siccome ρ deve essere maggiore di zero, otteniamo 0 ≤ ρ ≤ 1.
Gli estremi per ρ e θ sono quindi rispettivamente (0,1) e (0,2π).
E’ possibile calcolare la jacobiana e il suo determinante, ottenendo abρ.
Il cambio di variabile con coordinate ellittiche risulta essere il seguente:

Ripetiamo che gli estremi per ρ e θ sono quindi rispettivamente (0,1) e (0,2π).
Ora vediamo un esempio su questi cambi di variabile.
esempio 2
Prendiamo il seguente insieme e calcoliamo la sua area.
![]()
SOL:
Intanto disegniamo il nostro insieme. In pratica è un’intersezione tra il cerchio di raggio √17 e il semipiano delle x positive. Dunque, per dirlo in termini semplici, è un semicerchio che ha le x positive. La figura è questa:

Sappiamo inoltre che per calcolare l’area dobbiamo fare un integrale doppio di un “1” in dxdy.
Siccome l’insieme è molto simile ad un cerchio (è un semicerchio) potremmo pensare di usare le coordinate polari. Facciamo quindi questa sostituzione:
![]()
Conosciamo già dalla teoria il determinante della jacobiana: è pari a ρ.
Ora dobbiamo capire come si modifica l’insieme Ω dopo aver fatto la sostituzione. Per capirlo dobbiamo scrivere le due disequazioni che definiscono Ω mettendo al posto di “x” ρcos(θ) e al posto di “y” ρsin(θ).

Nella prima riga abbiamo “svolto” la prima disequazione: arrivati a ρ2 ≤ 17 facciamo la radice in entrambi i membri. Questo non è un passaggio convenzionale e in analisi 1 è una blasfemia (perché quando facciamo la radice dobbiamo scrivere anche un “±”) però ricordiamo che per definizione ρ>0 quindi di sicuro la parte negativa non va bene e possiamo fregarcene.
Nella seconda riga abbiamo tolto ρ perché è >0 e poi sappiamo che il coseno è positivo quando θ è compreso tra -π/2 e π/2.
Se guardate attentamente la figura precedente vi renderete conto che gli estremi che abbiamo trovato indicano proprio la regione rossa: l’angolo tra -π/2 e π/2 indica la parte a destra dell’asse y, mentre gli estremi di ρ indicano che prendiamo di sicuro un punto che sta dentro al cerchio (perché ρ deve essere minore del raggio del cerchio).
A questo punto scriviamo l’integrale, ricordandoci il determinante della jacobiana (che spesso si dimentica):
Come vedete, risulta un integrale molto semplice.
Con questo banale esercizio avete capito come utilizzare le coordinate polari. Per le ellittiche funziona allo stesso modo. Se avete una funzione f(x,y) dovete sostituire la x e la y di quella funzione e mettere ρcos(θ) e ρsin(θ). Quest’ultima cosa non l’abbiamo fatta perché stavamo integrando un “1”.
Abbiamo finito questa mega lezione. Nella prossima ci saranno gli integrali tripli.
Fai click su Lezione 21 per passare alla prossima lezione.
