In questa lezione vediamo la definizione di curva regolare, le curve planari, la lunghezza di un arco di curva e la definizione di curva rettificabile.
Curva regolare
Una curva r si dice regolare se valgono le seguenti proprietà (in cui I è il dominio della curva):
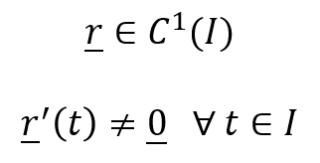
In pratica ci sta dicendo che la curva deve essere continua e derivabile con derivata continua, ma fornisce una condizione aggiuntiva: la derivata non deve mai essere uguale al vettore nullo. Ciò significa che voi potete avere qualche componente della derivata che si annulla, ma non devono annullarsi tutte le componenti della derivata.
Se per es. abbiamo che r’ = (t, t2), significa che per t=0 il vettore derivato diventa il vettore nullo. Quindi la curva non è regolare.
Ci sono anche delle curve che sono regolari a tratti, cioè sono formate da pezzi di curve regolari.
Curva regolare a tratti
Una curva r : I → Rn (come nella definizione precedente) è regolare a tratti se I può essere scritto come unione finita di sottointervalli, all’interno dei quali r è regolare.
Cosa vuol dire?
Se abbiamo una curva che in certi punti non è regolare, ma in cui il suo dominio si può dividere in un numero finito di intervalli in cui è regolare, essa è regolare a tratti.
In pratica abbiamo una curva, vediamo che non è regolare. Cerchiamo di capire se possiamo suddividerla in un numero finito di pezzetti in cui è regolare. Se ci riusciamo è regolare a tratti.
Per capire facciamo un esempio.
esempio 1
Abbiamo la seguente curva definita per t ∈ [0,2π]. Per comodità scriviamo anche la sua derivata, che è la derivata delle singole componenti:
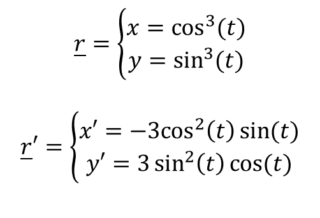
Per calcolare x’ e y’ abbiamo derivato rispettivamente x e y.
Ora ci domandiamo se è regolare. Cioè se esiste un valore di t che annulla contemporaneamente sia x’ sia y’. In tal caso verrebbe fuori r’ = (0,0) = 0 e quindi la curva non sarebbe regolare.
Siccome sia x’ che y’ hanno una moltiplicazione cos(t) e sin(t), nei valori in cui uno dei due si annulla avremo una r’ = 0. Mi spiego meglio: coseno e seno sono in entrambe le componenti e vengono moltiplicati tra loro. Per avere la prima componente nulla dovrei avere che o il cos(t) o il sin(t) si annulla. Per avere la seconda componente nulla dovrei ancora una volta avere che o il cos(t) o il sin(t) si annulla.
Siccome t è compreso tra 0 e 2π, i valori in cui coseno o seno si annullano sono: 0 (si annulla il seno), π/2 (si annulla il coseno), π (si annulla di nuovo il seno), 3π/2 (si annulla di nuovo il coseno), 2π (si annulla ancora il seno).
Per tutti questi valori di t la r’ sarà il vettore nullo e quindi in generale la curva che abbiamo scritto NON è regolare.
E’ regolare a tratti? Sì perché potremmo scrivere il dominio come un unione tra pezzi di curva che sono regolari. Come? Scriviamo [0, 2π] = (0,π/2) U (π/2,π) U (π,3π/2) U (3π/2,2π). In questo modo il dominio è suddiviso in diversi pezzi in cui la curva risulta regolare (perché non abbiamo messo gli estremi degli intervalli).
I punti in cui ci sono problemi vengono in pratica scelti come estremi degli intervalli e siccome tra quei punti la curva è regolare (perché in quegli intervalli t non può valere numeri che vanno ad annullare entrambe le componenti di r’ dato che abbiamo escluso gli estremi, che sono i punti problematici) si dice che è regolare a tratti.
Curva planare
Le curve planari sono curve che stanno su un piano, cioè quelle che riuscite a disegnare sul foglio, ovvero che sono in 2D.
Esse hanno solo due componenti ma adesso vediamo delle definizioni più serie.
Le curve planari si possono scrivere in due forme: cartesiana e polare. La prima è quella a cui siamo abituati, mentre la seconda è utile in certi casi.
forma cartesiana
Una curva r : I → R2 è scritta in forma cartesiana se è scritta in questo modo:
![]()
In questa formula, t ∈ I e f ∈ C1(I). Ciò significa che f è una qualsiasi funzione che sia continua e derivabile con derivata continua.
Da notare che x(t) = t.
Una curva scritta in forma cartesiana ha tre proprietà che elencheremo qui di seguito:
- Regolare
Essa è di sicuro regolare perché è di classe C1 (dato che x(t) è un polinomio e f è C1) e la sua derivata è di sicuro diversa dal vettore nullo perché x'(t) = 1. - Semplice
Essa è semplice, cioè la curva r è iniettiva. L’iniettività è abbastanza facile da verificare: iniettiva significa che presi due valori diversi di t si ottengono due valori diversi di r. Ciò è verificato di sicuro perché presi t1 e t2 diversi, quando guardiamo r(t1) e r(t2) troviamo la prima componente diversa (dato che in un caso sarà t1 e nell’altro t2, che sono diversi per ipotesi). Quindi otteniamo due vettori diversi.
Questo significa che la curva è iniettiva, quindi semplice. - Guardiamo il sostegno
Il sostegno di questa curva, siccome x(t) = t, è semplicemente il grafico y = f(x).
forma polare
Una curva r è scritta in forma polare se è scritta in questo modo:
![]()
Come vedete, le due componenti dipendono da ρ e da θ. La variabile ρ è una funzione che dipende solo da θ (infatti abbiamo scritto f(θ)).
Possiamo trovare la derivata della curva scritta in forma polare (sapendo che ρ=f(θ)):
![]()
A differenza della forma cartesiana, una curva in forma polare non è necessariamente regolare perché nessuno vi garantisce che x’ e y’ sono diverse da zero entrambe.
Lunghezza dell’arco di curva
Ora daremo la definizione di lunghezza di un arco di curva. Non preoccupatevi: è una definizione che fa pietà, serve solo per la teoria. Negli esercizi si usa il teorema che scriviamo dopo: quello è bello e ci salva la vita.
Consideriamo una curva r: [a,b] → Rn. Scriviamo l’intervallo [a,b] come unione di tanti intervalli diversi:
![]()
Approssimiamo la curva r con dei segmenti che vanno da r(a) ad r(t1), da r(t1) a r(t2) ecc.
La lunghezza della curva è l’estremo superiore delle lunghezze di tutte le possibili spezzate. In formule:
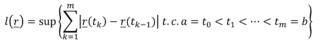
Da notare che abbiamo posto a=to e tm = b.
Non commenteremo questa formula. E’ una definizione e la prendiamo così com’è.
Adesso vediamo un teorema molto importante perché è quello che serve negli esercizi.
teorema: calcolo della lunghezza
Data una curva r: [a.b] → Rn regolare, la lunghezza della curva si calcola così:
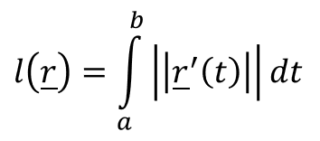
Vediamo un esempio.
esempio 2
Prendiamo una curva scritta in forma cartesiana. La sua derivata è questa (calcolata derivando ogni componente):
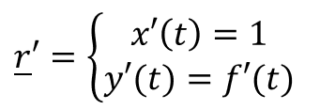
La norma di questa r’ è facile da calcolare:
![]()
Adesso per calcolare la lunghezza della curva r basta solo integrare tra a e b la norma di r’.
Tutto bellissimo.
ATTENZIONE: il teorema non si può applicare alle curve regolari a tratti.
Curva rettificabile
Una curva è rettificabile se la sua lunghezza esiste ed è finita.
Se una curva è unione di tante curve rettificabili, allora essa è rettificabile e la sua lunghezza è pari alla somma delle lunghezze delle curve di cui è unione.
ATTENZIONE: la lunghezza di una curva non coincide sempre con la lunghezza del suo sostegno.
Ora vediamo un esempio per capire il concetto.
esempio 3
Prendiamo la seguente curva (di cui scriviamo anche la derivata), con t ∈ [0,7π].
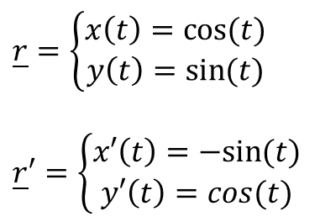
La curva, se la tracciate sul piano cartesiano, disegna una circonferenza perché man mano che t cresce la x e la y sono rispettivamente il coseno e il seno di t. Provate a buttare dentro dei valori di t, a calcolare x e y e a disegnare i punti che ottenete sul piano cartesiano: viene fuori una circonferenza.
La circonferenza è il sostegno della curva (perché è il suo grafico) e sappiamo che è lunga 2π.
Tuttavia se calcoliamo la lunghezza della curva otteniamo:
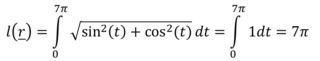
La morale è che la lunghezza del sostegno è 2π ma la lunghezza della curva è 7π. Quest’ultimo valore dipende dal dominio della curva (che nel nostro caso dice t ∈ [0,7π]).
State quindi attenti: nel dubbio calcolate la lunghezza della curva con la formula del teorema visto poco fa e non guardate la lunghezza del grafico che avete disegnato.
Per passare alla prossima stupenda lezione clicca qui.
